Somos estudiantes de licenciatura en desarrollo de software de la Universidad Tecnológica De Panamá sede regional de Chiriquí y nos corresponde la creación de este blog educativo en donde desarrollaremos el tema de "la derivada".
Los punto que trataremos son los siguientes:
v La derivada
Ø Interpretación geométrica de la derivada
§ Recta tangente y normal
Ø Definición de derivada
Ø Derivada de funciones algebraicas
Ø Derivadas de funciones trigonométricas
interpretación geométrica de la recta
interpretación geométrica de la recta
Recta tangente a una curva en un punto
La noción de Euclides de una tangente, como una recta que toca a una curva en un solo punto es totalmente correcta para circunferencias ; pero completamente insatisfactoria para otras curvas . La idea de una tangente, en P a una curva como la recta que mejor se aproxima a la curva cerca de P es bastante mejor, pero aun muy vaga para la precisión matemática. El concepto de límites proporciona una manera de obtener una mejor descripción. Sea P un punto en una curva y sea Q un punto móvil cercano a P en esa curva. Considere la recta que pasa por P y Q llamada recta secante. La recta tangente en p es la posición limite (si esta existe) de la recta secante cuando Q se mueve hacia p a lo largo de la curva .
Suponga que la curva es la grafica de la ecuación Y=f(x). Entonces P tiene coordenadas (c,f(c)), un punto cercano Q tiene coordenadas (c+h,f(c+h)), y la recta secante de P y Q tiene pendiente msec dada por :



La derivada de una función f(x) en un punto x = a es el valor del límite, si existe, del cociente incremental cuando el incremento de la variable tiende a cero.


cambio de notación
Recta normal a la curva en un punto
se llama recta normal a una curva en un punto, la recta perpendicular a la recta tangente en ese punto. en la siguiente figura se muestra la recta normal:
Ecuación de la recta normal
La recta normal a a una curva en un punto a es aquella
que pasa por el punto (a, f(a)) y cuya pendiente es igual a
la inversa de la opuesta de f '(a).
definición de derivada
Reglas de derivación
Derivada de una constante
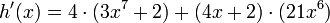
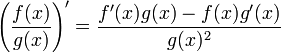
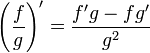


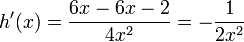
Derivadas de funciones trigonométricas
fuentes: http://www.dervor.com/index.html
http://es.wikipedia.org/wiki/Reglas_de_derivaci%C3%B3n
Bibliografía: Calculo diferencial e integral; Purcell, Varberg,Rigdon.
novena edición
Derivada de una constante
Una función polinómica de grado 0 o función constante es aquella que no depende de ninguna variable y su derivada siempre será cero.
Si f(x) = a , tendremos que f'(x) = 0
Donde a es una constante, como un ejemplo:
f(x) = 7
f'(x) = 0
Derivada de una potencia entera
Una función potencial con exponente entero se representa por f(x) = xn y su derivada es f'(x) = nxn − 1.
Por ejemplo tomemos la función:
f(x) = x3
Lo primero que se debe hacer es "bajar" el exponente de tal forma que éste multiplique a la variable con respecto a la cual estamos derivando, luego al mismo exponente se le resta la unidad formando uno nuevo, así:
f'(x) = 3x3 − 1
Quedando finalmente:
f'(x) = 3x2
Derivada de una constante por una función
Cuando una función esté representada por medio de f(x) = cxn, su derivada equivale a f'(x) = n(cx(n − 1)) de la siguiente manera:
Consideremos la siguiente función: f(x) = 8x4, lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:
f'(x) = 4(8x4 − 1)
Para obtener
f'(x) = 32x3
Cuando una constante acompaña a una variable cuyo exponente es 1 su derivada será el valor de la constante:
f(x) = 7x
Entonces su derivada con respecto a esta variable será:
f'(x) = 7
Puesto que x0 = 1
Derivada de una suma
Se puede demostrar a partir de la definición de derivada, que la derivada de la suma de dos funciones es la suma de las derivadas de cada una.
Es decir, (f + g)'(x) = f'(x) + g'(x) o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
Como ejemplo consideremos la función f(x) = 3x5 + x3, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
f'(x) = 15x4 + 3x2
Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función"
Y matemáticamente expresado por la relación 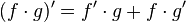 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:
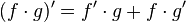 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:
h(x) = (4x + 2)(3x7 + 2)
Identificamos a f(x) = (4x + 2) y g(x) = (3x7 + 2), utilizando las reglas anteriormente expuestas, vemos que:
f'(x) = 4 y que g'(x) = 21x6
Por lo tanto
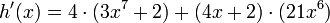
Simplificando y organizando el producto obtenido nos queda
h'(x) = 84x7 + 12x7 + 42x6 + 8
Sumamos términos semejantes y finalmente obtenemos la derivada:
h'(x) = 96x7 + 42x6 + 8
Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir 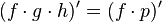 en donde
en donde 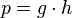 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).
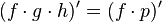 en donde
en donde 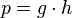 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).Derivada de un cociente
La derivada de un cociente se determina por la siguiente relación:
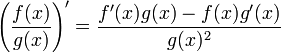
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
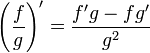
Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es g(x) = 2x y se multiplique por la derivada del numerador que seria f'(x) = 3; luego la segunda parte dice que tomemos la función del numerador (f(x)) sin derivar y lo multipliquemos por la derivada de g(x) = 2x, que seria g'(x) = 2, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:
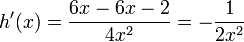
Derivadas de funciones trigonométricas
Problemas propuestos
http://es.wikipedia.org/wiki/Reglas_de_derivaci%C3%B3n
Bibliografía: Calculo diferencial e integral; Purcell, Varberg,Rigdon.







